A definite integral of a function can be represented as the signed area of the region bounded by its graph:

A function f of a real variable x and an interval [a, b] of the real line, definite integral:
 or
or 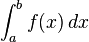 if the domain is an interval [a, b] of x;
if the domain is an interval [a, b] of x;
The term integral may also refer to the notion of the antiderivative, a function F whose derivative is the given function f. In this case, it is called an indefinite integral and is written:
General formula:
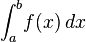

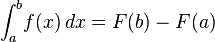
Aucun commentaire:
Enregistrer un commentaire